Construct an Archimedean Spiral of one convolution, given the maximum and minimum radii as 55 mm and 31 mm respectively. Draw tangent and normal to the curve at any point.

Vishal R. Pawar May 16, 2022

Archimedean Spiral

In this post, we'll learn about how can we draw an Archimedean Spiral very easily! We'll understand the method by solving the given question:

Question: Construct an Archimedean Spiral of one convolution, given the maximum and minimum radii as 55 mm and 31 mm respectively. Draw tangent and normal to the curve at any point.

Solution:

Constant of curve (C.O.C) = (R - r) / (2𝜋 × No. of convolution)

= (55 - 31) / (2𝜋 × 1)

= 3.82 mm

Procedure:

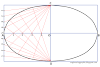
Draw two monocentric circles of radius 55 mm and 31 mm and divide them into 8 equal parts.
Divide the line HH' into 8 equal parts and name them as shown in the figure. (Don't know how to divide a line into equal parts? To know follow the link - How to divide a line into equal parts?)
Take distance O1 in a compass and mark a point on the line OA and name it 1'.
Now take O2 distance and mark a point on the line OB and name it 2'.
Take O3 distance and mark a point on the line OC and name it 3'.
Like this mark all the rest of the points (4', 5', 6' & 7').
Connect all the points (H, 1', 2', 3', 4', 5', 6', 7' and 8) with a smooth curve with the help of a french curve.
Your Archimedean Spiral is ready.
Now to draw tangent and normal to the spiral, follow the point given below:
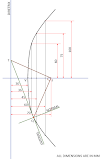
Take a random point on the curve and name it Q.
Connect the points Q and O with a straight line.
Draw a perpendicular line of 3.82 mm (C.O.C) from point O. Name the line ON.
Connect points Q and N. This line will be the normal of the curve.
Draw a perpendicular line to line QN on point Q. This line will be the tangent of the curve.
Don't forget to show all the necessary dimensions.

I hope you understood the solution. If you have any doubts regarding the question or solution, just ask me in the comment section! Till then keep learning, and keep improving!