How to draw Tangent & Normal to an Epicycloid?

Tangent & Normal to An Epicycloid

In this post, we'll learn about how can we draw normal and tangent to an epicycloid. For example, we'll draw normal and tangent to an epicycloid according to the given question.

Question: A circle of 50 mm diameter rolls on the circumference of another circle of 180 mm diameter and outside it. Trace the locus of a point on the circumference of the rolling circle, for one complete revolution. Name the curve formed. Draw a tangent to the curve at a point on it 125 mm from the center of the directing circle.

Solution:

Procedure:

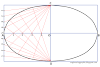
1. Draw an Epicycloid according to the given data. (Don't know how to draw an epicycloid? To learn, kindly follow the given link: How to draw an Epicycloid?)
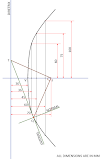
2. Take a point on the epicycloid and name it Q.
3. From the point, Q draw an arc of 25 mm on the arc passing through the center of the circle. 
4. From that point, draw a straight line to the center of the circle having a 90 mm radius (180 mm diameter).
5. At where the straight line intersects the bigger circle, name that point N.
6. Draw line QN, which will be the Tangent to the given epicycloid.
7. Draw a perpendicular line to the line QN, which will be the Tangent to the given curve.

I hope you understood the concept. If you have any doubts regarding the method, just let me know in the comment section! Till then keep learning, and keep improving!

Similar Questions:

• Draw an involute of a regular pentagon of side 20 mm.
  
• Construct an Archimedean Spiral of one convolution, given the maximum and minimum radii as 55 mm and 31 mm respectively. Draw tangent and normal to the curve at any point.