How to draw an Epicycloid?

Epicycloid

In this post, we'll learn about how we can draw an epicycloid. For example, we'll draw an epicycloid according to the given question.

Question: A circle of 50 mm diameter rolls on the circumference of another circle of 180 mm diameter and outside it. Trace the locus of a point on the circumference of the rolling circle, for one complete revolution.

Solution:

Procedure:

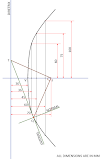
• Ⲑ = (d/D) ✕ 360° = (50 / 180) ✕ 360° = 100°
• According to the above equation, draw an angle of 100 degrees of 90 mm long side.

• As shown in the solution, draw an arc of 90 mm radius taking O as a centre.
• As shown in the figure, draw a circle of 50 mm diameter on the top of the arc. Divide it into 8 equal parts and name it as per the figure.
• Because we divide the circle into 8 equal parts, Divide the 100-degree angle into 8 equal parts too.
• Draw arcs passing through points 7 and 1 as well as 6 and 2, 5 and 3, and 4 taking O as the centre. Also, draw an arc passing through the centre of the circle O'.
• Name all the points as shown in the solution.
• Take a 25 mm radius in a compass and draw an arc on the arc71 taking the centre as the C1 point. Name it A.
• Now, draw an arc on the arc62 taking the centre as point C2, and name it B.
• Likewise draw all the remaining arcs (C, D, E, F, G, and H) as shown in the figure.
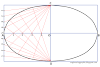
• Connect all the points (A to H) with a smooth curve.
• Your epi cycloid is ready.

I hope you understood the concept. You can draw any kind of Epicycloid by just following the given method. If you have any doubts regarding the method, just let me know in the comment section! Till then keep learning, and keep improving!

Similar Questions:

• How to draw Tangent & Normal to an Epicycloid?
  
• Draw an involute of a regular pentagon of side 20 mm.
  
• Construct an Archimedean Spiral of one convolution, given the maximum and minimum radii as 55 mm and 31 mm respectively. Draw tangent and normal to the curve at any point.