Draw a curve whose vertex is 30 mm from its directrix and whose eccentricity is 5/3. Name the curve. Draw the normal and tangent to the curve at a point 25 mm from the directrix.

 Hyperbola

In this post, we'll learn about how can we draw a hyperbola. For example, we'll draw a hyperbola according to the given question.

 

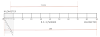
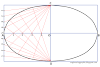
Question: Draw a curve whose vertex is 30 mm from its directrix and whose eccentricity is 5/3. Name the curve. Draw the normal and tangent to the curve at a point 25 mm from the directrix.

Solution:

Hyperbola

Procedure: 

1. Draw a hyperbola. To know how to draw a hyperbola, click here.  
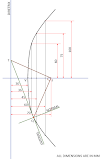
2. Join points Q and F.
3. Construct a 90° angle with this line at point F.
4. Extend the line to meet directrix at T tangent to curve from Q.
5. To this tangent draw a perpendicular line from Q. It is normal to the curve.  

I hope you understood the concept. You can draw any kind of hyperbola by just following the given method. If you have any doubts, just let me know in the comment section! Till then keep learning, keep improving

Similar Questions:

1. Point F is 50 mm from line AB. point P is moving in a plane such that the ratio of its distances from F and line AB remains constant and equal to 2/3. draw locus of point P. { ECCENTRICITY = 2/3 }