Find M of a line MN, which is inclined at 46° to H.P. and 20° to V.P. is 15 mm above the H.P. and it is in front of the V.P., while the end N is 60 mm in front of V.P. and is above H.P. Draw the projections of the line, find its true length if its plan length is 70 mm. Locate the points of intersection of the line with the principal planes.

Projection Of Lines

Question: Find M of a line MN, which is inclined at 46° to H.P. and 20° to V.P. is 15 mm above the H.P. and it is in front of the V.P., while the end N is 60 mm in front of V.P. and is above H.P. Draw the projections of the line, find its true length if its plan length is 70 mm. Locate the points of intersection of the line with the principal planes.

Given Data:

• θ = 46°
• ɸ = 20°
• m' = 15 mm above HP
• n = 60 mm in front of VP
• TVL = 70 mm

Solution: 

Procedure:

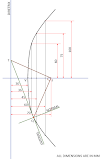
• Project the point m' according to the question (Don't know the concept of Projection of Points? Don't worry click here to learn!) and draw the locus of n 60 mm (= 6 cm) below the XY line.
• Draw a vertical line at the distance of 70 mm (= 7 cm) from the point m' (Because TVL (Top View Length) is 70 mm (= 7 cm)).
• Now for the true length, draw a line at the inclination of 46° from the point m'. Where the vertical line and the inclined line intersect, name that point n₁'. Also, draw the locus of n'.
• Connect the points m' and n₁' which is the true length of the line MN. Measure the length of the line which should be equal to 100 mm (= 10 cm).
• Now, to find the position of the point m, draw a line at the inclination of 20° at XY line as shown in the solution.
• Take a roller scale and put it parallel to the inclined line which you drew in the last step.
• Roll down the scale until the distance between the locus of n and the vertical line (in green color shown in the solution) becomes exactly 100 mm (= 10 cm).
• Draw a line at that position of 100 mm (= 10 cm) which is the true length of the line MN.  
• Where that line and vertical line (in green color shown in the solution) intersect, name that point m. Also, draw the locus of m.
• To make the top view of the line MN, draw an arc of 70 mm taking the center as the point m, to the locus of n.
• Where they intersect, name that point n and connect the points m and n. Which is the top view of the line MN.
• To draw the front view, draw a vertical line from the point n to the locus of n'. Where they intersect, name that point n'.
• Connect the points m' and n' which is the front view of the line MN.
• Show all the necessary dimensions as shown in the solution.

Asked Data:

• TL = 100 mm
• m = 25 mm in front of the VP

I hope you understood the solution and the procedure. If you have any doubts regarding the solution or the question, let me know in the comment section. Till then keep learning, and keep improving!

Similar Questions:

1. The elevation of line AB, 80 mm long, measures 55 mm. The end A is 20 mm above H.P. and 10 mm in front of V.P. Draw the projections of the line and find its true inclinations with H.P. and V.P. If the end B is 25 mm below H.P. and is behind V.P.
   
2. A straight line AB is 60 mm long. It is inclined to H.P. and V.P. by an angle of 30° and 45° respectively. Point A is 30 mm above H.P. and 20 mm in front of V.P. Draw the projections of straight line AB. Find also the traces.
   
3. Draw the projections of the following points on the same x-y line. 1) Point A on V.P. and 30 mm below H.P. 2) Point B on H.P. and 20 mm in front of V.P. 3) Point C 20 mm above H.P. and 20 mm behind V.P. 4) Point D 25 mm below H.P. and 40 mm behind V.P. 5) Point E on H.P. and on V.P. 6) Point F 40 mm above H.P. and 10 mm in front of V.P. 7) Point G on V.P. and 35 mm above H.P.