A regular pentagon of 50 mm sides is resting on one of its sides on the H.P. such that it is parallel to and 25 mm in front of the V.P. If the highest corner of the pentagon rests in the V.P., draw its projections and find the angle made by the plane with the H.P.

 Projection Of Plane

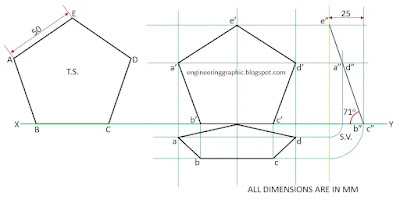
Question: A regular pentagon of 50 mm sides is resting on one of its sides on the H.P. such that it is parallel to and 25 mm in front of the V.P. If the highest corner of the pentagon rests in the V.P., draw its projections and find the angle made by the plane with the H.P.

Solution:

Explanation:

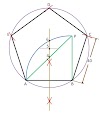
• In the last line of the question, you are told to find the angle made by the pentagonal plane with the H.P. (Horizontal Plane). So, to determine the angle you need to draw its side view.
• As the question suggests, a pentagon is parallel to the V.P. (Vertical Plane) and 25 mm (= 2.5 cm) in front of the V.P. Also its highest corner is resting on the V.P. It means the front view, top view and the side view should be like the given solution.

Procedure:

• First, draw the true shape of the pentagon. 
• To draw the side view, draw a vertical line and choose a point 25 mm ahead of the vertical line on the XY line (Because the pentagon is 25 mm ahead of the vertical plane).
• Draw an arc exactly of the height of the pentagon (From line BC to point E) from that point (25 mm ahead of the vertical line), on the vertical line. 
• Connect that point and the intersection of the arc and vertical line with a straight line. Which is the side view of the pentagon.
• With the help of the projections of the side view, draw the front view and the top view of the pentagon.

I hope you understood the explanation and the solution very well. If you have any doubts, let me know in the comment section. Till then keep learning, and keep improving!

Similar Questions:

1. A square plate of side 60 mm is held on a corner on HP. The plate is inclined to the HP such that the plan of it is rhombuses with a diagonal of 30 mm. Determine the angle it makes with HP. The other diagonal is inclined at 45˚ to VP. Draw the projections of the plate.
2. A regular hexagonal plate 30 mm side is resting on one of its corners in V.P. the diagonal through that corner is inclined at 40° to V.P. and (i) if diagonal is inclined at 30° to H.P. (ii) if the plan of diagonal is inclined at 30° to H.P.